用户购买价格:5金币 本套试题答案购买后显示 购买本答案
(数学里面公式只能以图片形式显示)
【上面答案为下列试题答案,请核对试题后再购买】www.botiku.com零号电大

高等数学基础第三次作业
第4章 导数的应用
(一)单项选择题
⒈若函数 满足条件( ),则存在 ,使得 .
A. 在 内连续
B. 在 内可导
C. 在 内连续且可导
D. 在 内连续,在 内可导
⒉函数 的单调增加区间是( ).
A. B.
C. D.
⒊函数 在区间 内满足( ).
A. 先单调下降再单调上升 B. 单调下降
C. 先单调上升再单调下降 D. 单调上升
⒋函数 满足 的点,一定是 的( ).
A. 间断点 B. 极值点
C. 驻点 D. 拐点
⒌设 在 内有连续的二阶导数, ,若 满足( ),则 在 取到极小值.
A. B.
C. D.
⒍设 在 内有连续的二阶导数,且 ,则 在此区间内是( ).
A. 单调减少且是凸的 B. 单调减少且是凹的
C. 单调增加且是凸的 D. 单调增加且是凹的
(二)填空题
⒈设 在 内可导, ,且当 时 ,当 时 ,则 是 的 点.
⒉若函数 在点 可导,且 是 的极值点,则 .
⒊函数 的单调减少区间是 .
⒋函数 的单调增加区间是 .
⒌若函数 在 内恒有 ,则 在 上的最大值是 .
⒍函数 的拐点是 .
(三)计算题
⒈求函数 的单调区间和极值.
⒉求函数 在区间 内的极值点,并求最大值和最小值.
⒊求曲线 上的点,使其到点 的距离最短.
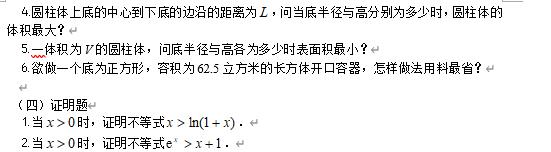
⒋圆柱体上底的中心到下底的边沿的距离为 ,问当底半径与高分别为多少时,圆柱体的体积最大?
⒌一体积为V的圆柱体,问底半径与高各为多少时表面积最小?
⒍欲做一个底为正方形,容积为62.5立方米的长方体开口容器,怎样做法用料最省?
(四)证明题
⒈当 时,证明不等式 .
⒉当 时,证明不等式 .
|
|
