一、单项选择题（共 10 道试题，共 100 分。）
1. 设函数f：N?N，f(n)=n+1，下列表述正确的是（ ）． A. f存在反函数
B. f是双射的
C. f是满射的
D. f 是单射函数
2. 设A={a，b，c}，B={1，2}，作f：A→B，则不同的函数个数为（ ）．
A. 2
B. 3
C. 6
D. 8
3. 设集合A={a}，则A的幂集为( )． A. {{a}}
B. {a，{a}}
C. {
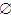，{a}}
D. {
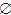，a}
4. 设A、B是两个任意集合，侧A-B = ?? ( )． A. A=B
B. A?B
C. A?B
D. B=?
5. 设集合A = {1, 2, 3, 4, 5}上的偏序关系的哈斯图如右图所示，若A的子集B = {3, 4, 5}，则元素3为B的（ ）．
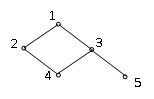
A. 下界
B. 最小上界
C. 最大下界
D. 最小元
6. 如果R1和R2是A上的自反关系，则R1∪R2，R1∩R2，R1-R2中自反关系有（ ）个． A. 0
B. 2
C. 1
D. 3
7. 设集合A={1, 2, 3}，B={3, 4, 5}，C={5, 6, 7}，则A∪B–C =( )．
A. {1, 2, 3, 4}
B. {1, 2, 3, 5}
C. {2, 3, 4, 5}
D. {4, 5, 6, 7}
8. 设集合A={1 , 2 , 3 , 4}上的二元关系R={<1, 1>，<2, 2>，<2, 3>，<4, 4>}，S={<1, 1>，<2, 2>，<2, 3>，<3, 2>，<4, 4>}，则S是R的（ ）闭包． A. 自反
B. 传递
C. 对称
D. 自反和传递
9. 设集合A = {1, a }，则P(A) = ( )． A. {{1}, {a}}
B. {
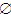,{1}, {a}}
C. {{1}, {a}, {1, a }}
D. {
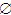,{1}, {a}, {1, a }}
10. 设A={a，b}，B={1，2}，C={4，5}，从A到B的函数f={, }，从B到C的函数g={<1，5>, <2，4>}，则下列表述正确的是（ ）． A. f°g ={, }
B. g° f ={, }
C. f°g ={<5，a >, <4，b >}
D. g° f ={<5，a >, <4，b >}
|
登录
立即咨询】